Mathematik - Klasse 5 bis 12

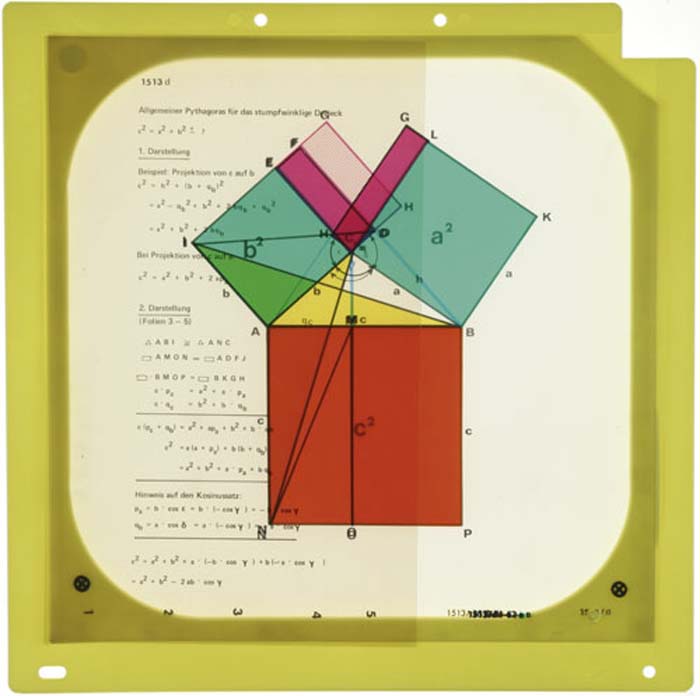
Scherung und Dehnung - Spitzwinkliges Dreieckfür den Overheadprojektor

Scherung und Dehnung - stumpfwinkliges Dreieckfür den Overheadprojektor

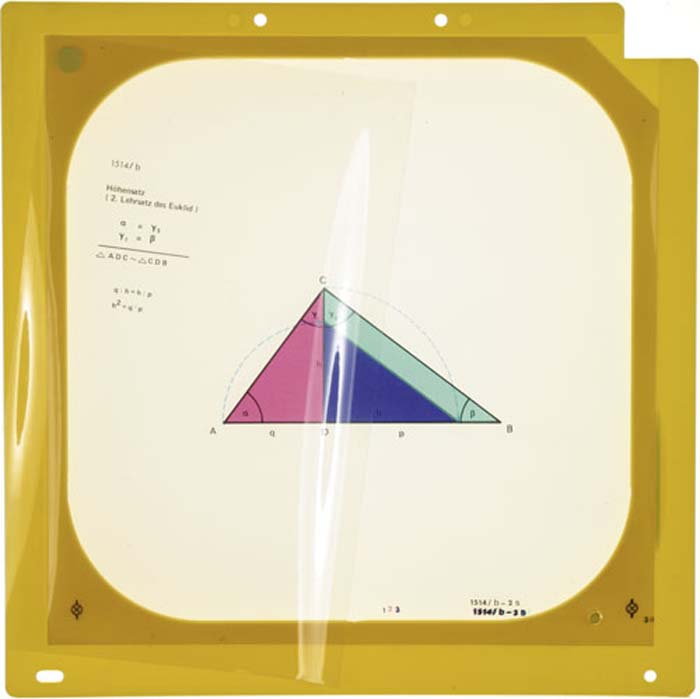
Ähnliche Dreiecke zum Beweis des Höhensatzes (2. Lehrsatz des Euklid).für den Overheadprojektor

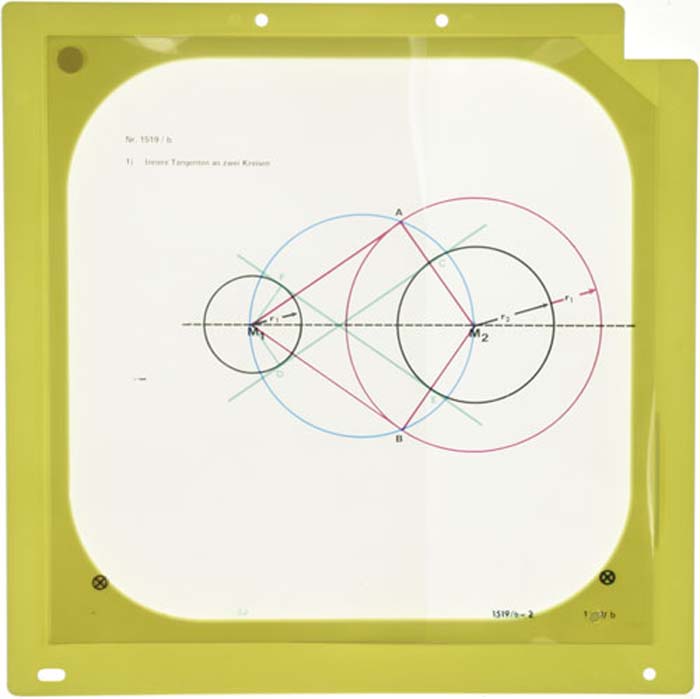
Tangenten an zwei Kreisen - Innere Tangentenfür den Overheadprojektor

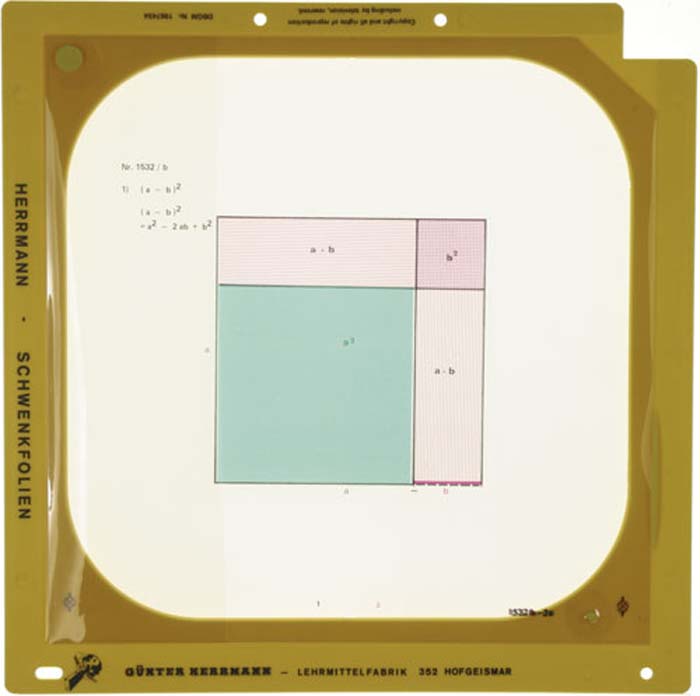
(a-b)²,für den Overheadprojektor(a-b)², für den Overheadprojektor

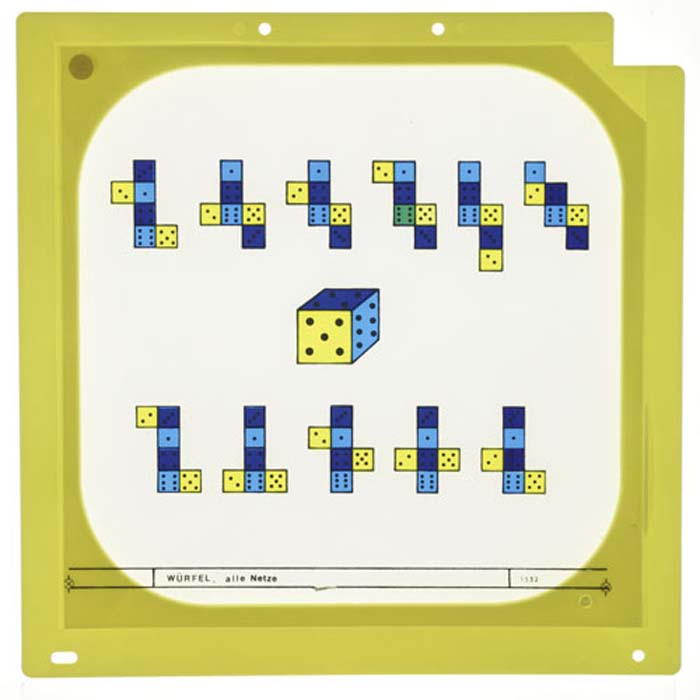
Stereometrie und Trigonometrie - Würfel: Alle Netzefür den Overheadprojektor

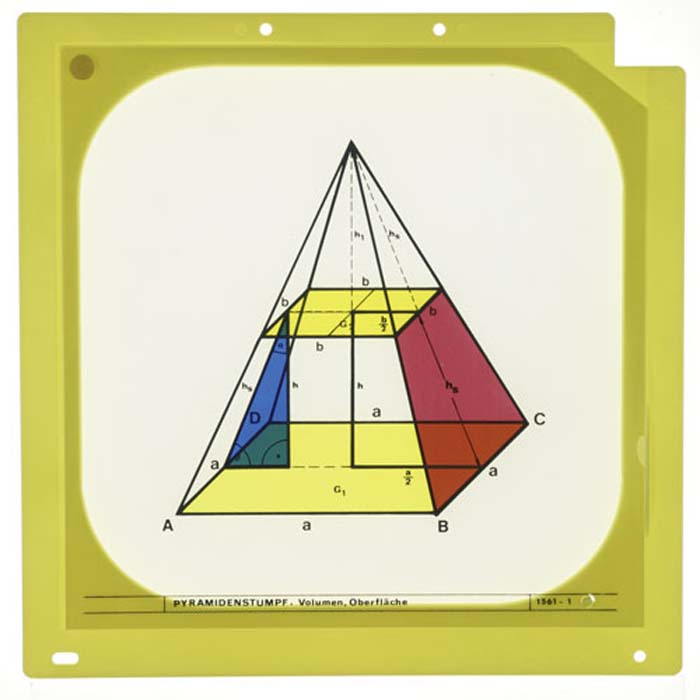
Stereometrie und Trigonometrie - Pyramidenstumpf: Oberfläche und VolumenOberfläche und Volumen, für den Overheadprojektor

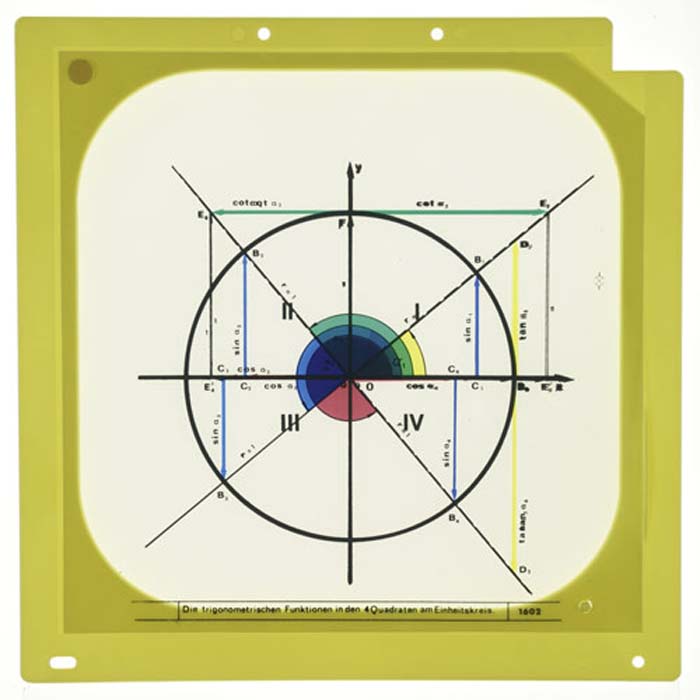
Stereometrie und Trigonometrie - Funktionen in den vier Quadraten am Einheitskreisam Einheitskreis, für den Overheadprojektor

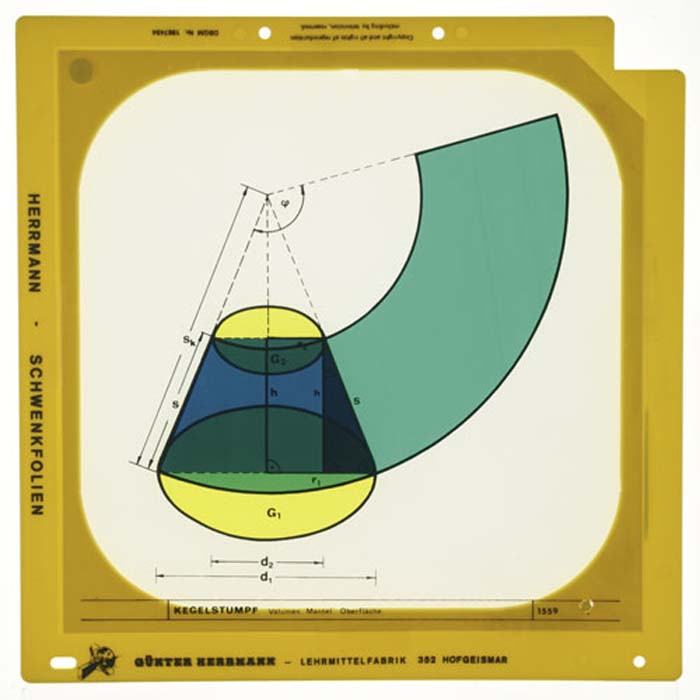
Stereometrie und Trigonometrie - Kegelstumpf: Volumen, Mantel, OberflächeVolumen, Mantel, Oberfläche, für den Overheadprojektor

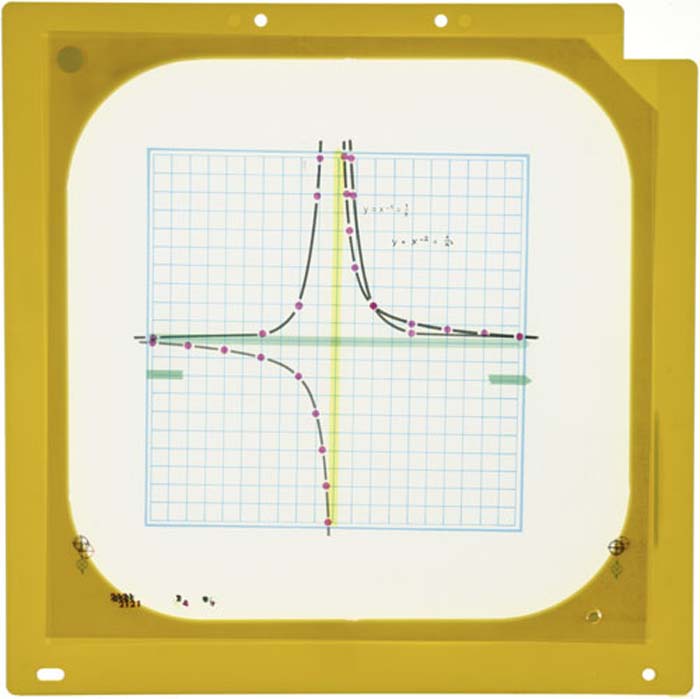
Potenzfunktionen: y = x-1 und y = x-2y = x-1 und y = x-2, für den Overheadprojektor

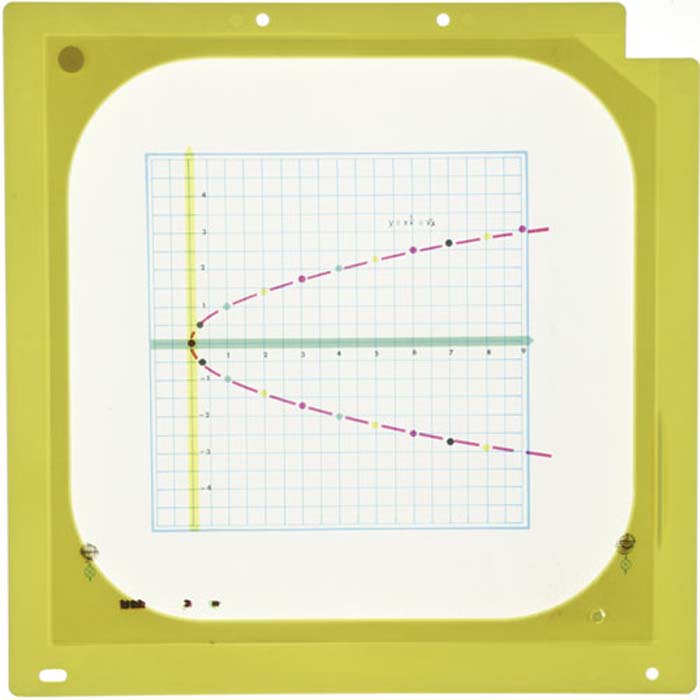
Potenzfunktion - y = x½y = x½, für den Overheadprojektor

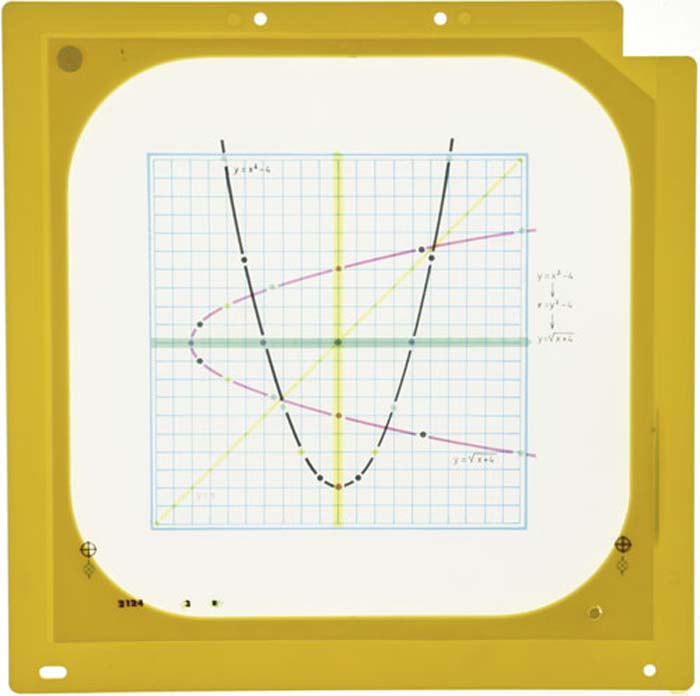
Wurzelfunktionen als Spiegelung der Potenzfunktionen - y = x²-4 und y = (x+4)½y = x²-4 und y = (x+4)½, für den Overheadprojektor

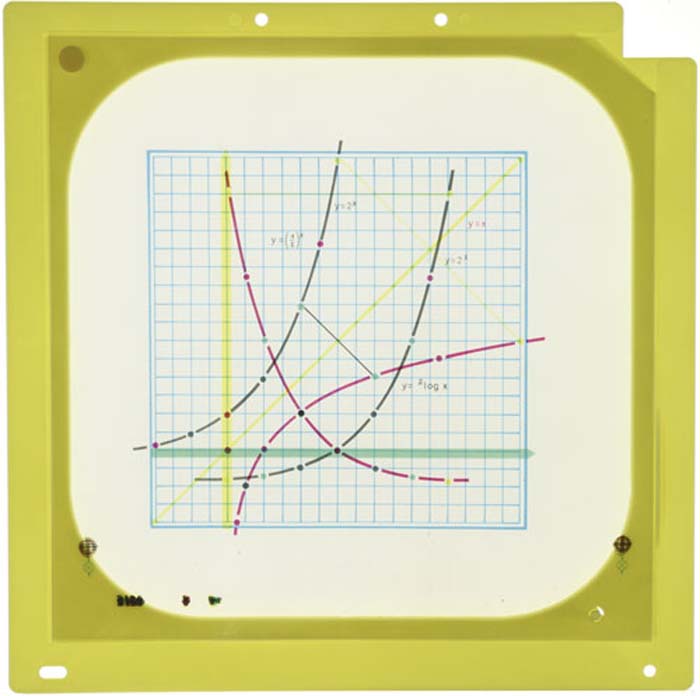
Logarithmische Funktionen als Spiegelung der Exponentialfunktion - y = 2x und y = (1/2)x sowie y = log2xy = 2x und y = (1/2)x sowie y = log2x, für den Overheadprojektor

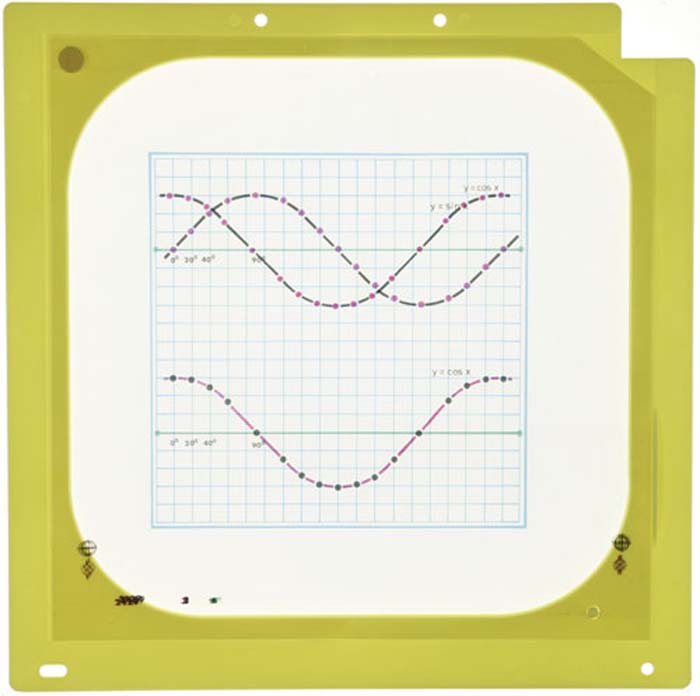
Trionometrische Funktion - y = sin x und y = cos xy = sin x und y = cos x, für den Overheadprojektor

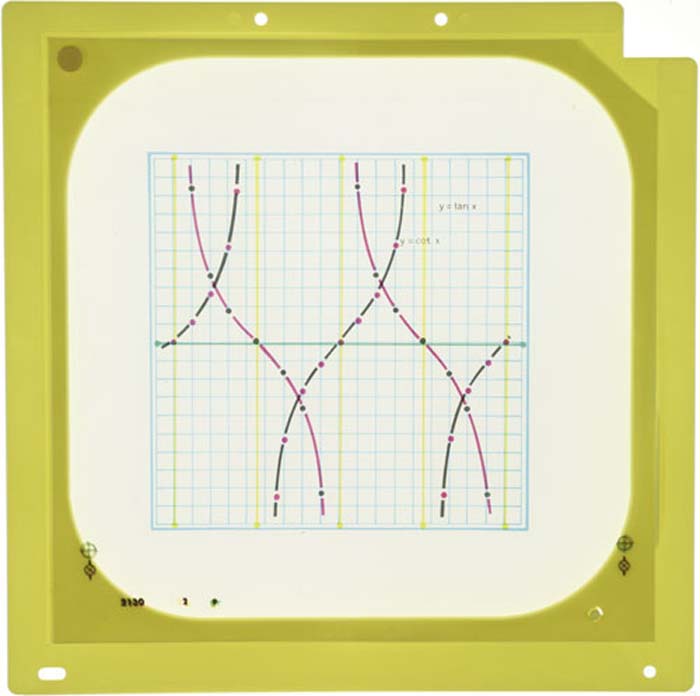
Trionometrische Funktion - y = tan x und y = cot xy = tan x und y = cot x, für den Overheadprojektor

Demonstrationsmodell für das Sehnenviereck.Im Sehnenviereck ergänzen sich gegenüberliegende Winkel stets zu 180°.Modell aus Plexiglas, hochwertiger Kunststoff.

Projektionsmodell für die Flächenverwandlung durch Scherung um einen parallel verschiebbaren Punkt.Modell aus Plexiglas, hochwertiger Kunststoff.

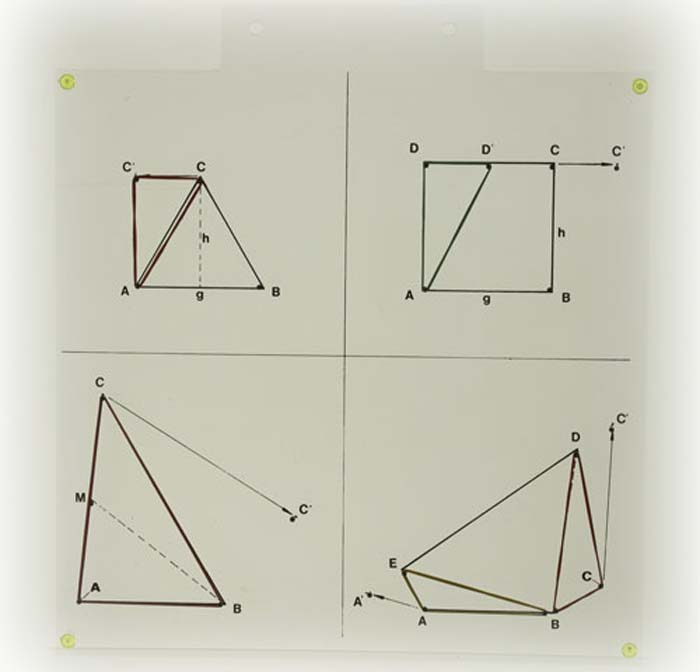
Projektormodell für die Flächenberechnung durch Scherung.Modell aus Plexiglas, hochwertiger Kunststoff.durch Scherung

Projektionsmodell für Bruchrechnung, Multiplikation und Division.Modell aus Plexiglas, hochwertiger Kunststoff.Multiplikation und Division.

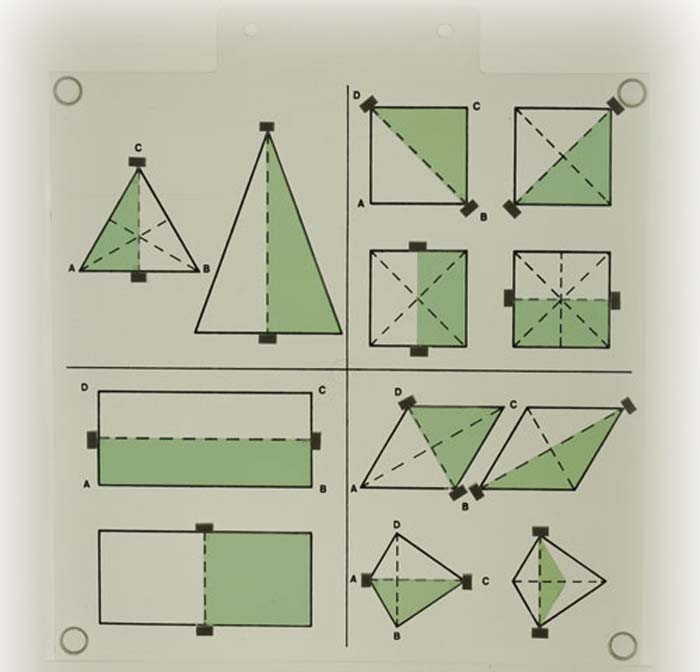
Projektionsmodell zur Veranschaulichung der Spiegelung und Achsensymmetrie.Modell aus Plexiglas, hochwertiger Kunststoff.und Achsensymmetrie

Projektor-Modell zur Darstellung einer Orthozykloide (gemeine).Modell aus Plexiglas, hochwertiger Kunststoff.(gemeine)

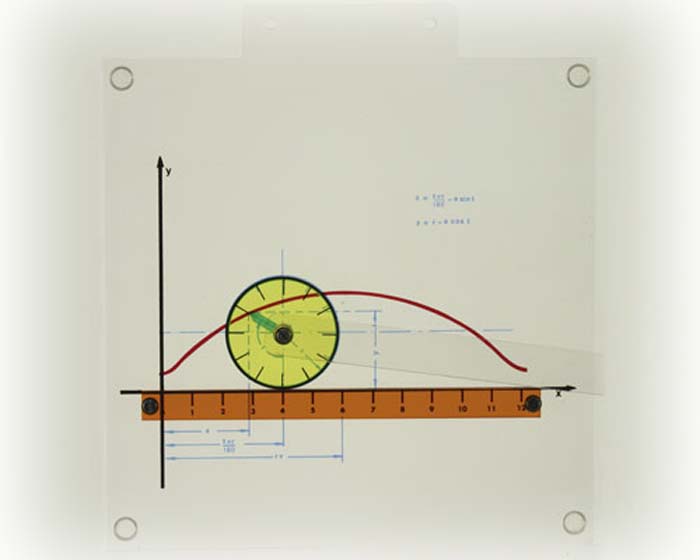
Projektor-Modell zur Darstellung einerOrthozykloide (verkürzt).Modell aus Plexiglas, hochwertiger Kunststoff.(verkürzt)

Projektor-Modell zur Darstellung einerOrthozykloide (verlängert).Modell aus Plexiglas, hochwertiger Kunststoff.(verlängert)

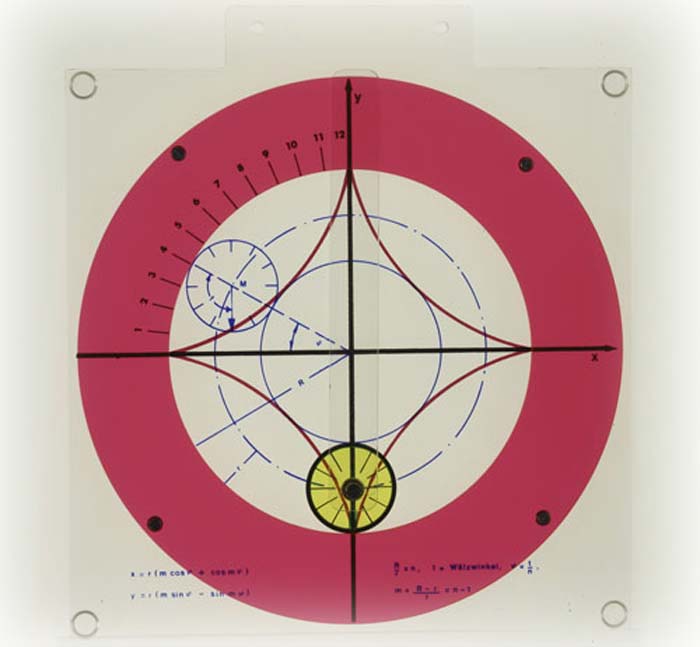
Projektor-Modell zur Darstellung einer Hypozykloide.Modell aus Plexiglas, hochwertiger Kunststoff.

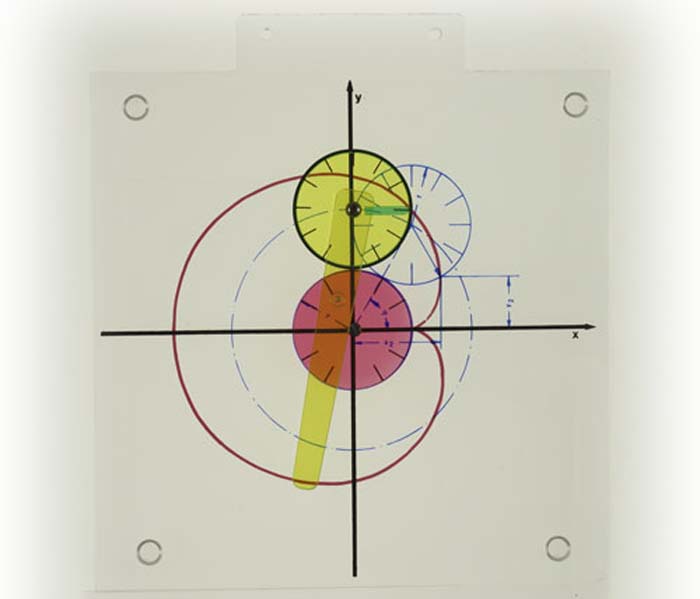
Projektor-Modell zur Darstellung einer Kardioide.Modell aus Plexiglas, hochwertiger Kunststoff.

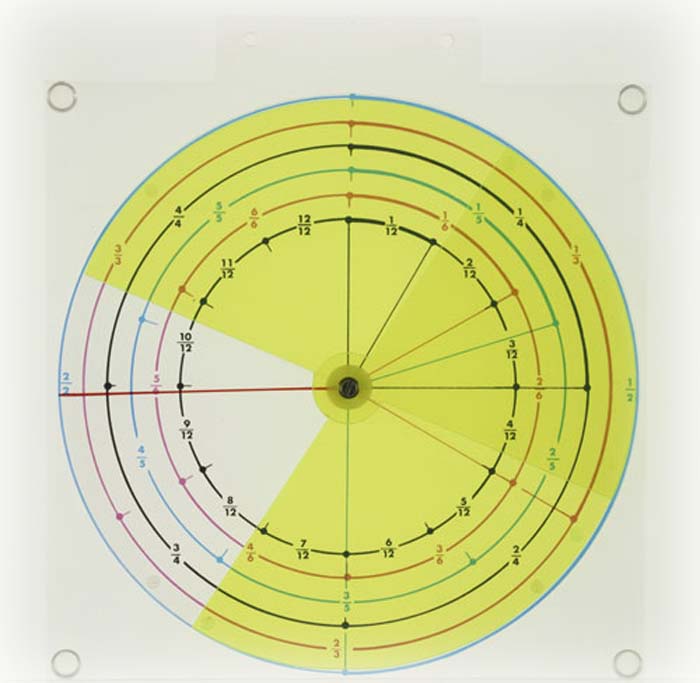
Bruchrechnungstafel für den Zahlenraum von 0 bis 1. Zwei farbige, gegeneinander drehbare Halbkreise ermöglichen die Behandlung folgender Bruchrechnungsarten: Erweitern, Kürzen, Addition, Subtraktion, Multiplikation und Division.Modell aus Plexiglas, hochwertiger Kunststoff.für den Zahlenraum von 0 bis 1

Projektor-Modell zur Darstellung eines Tangentenvierecks.Die Summe zweier gegenüberliegender Seiten des Tangentenvierecks ist konstant. Modell aus Plexiglas, hochwertiger Kunststoff.

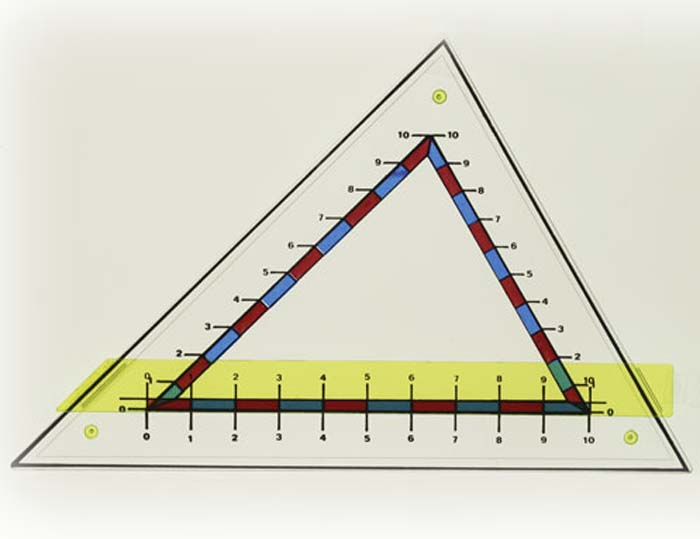
Projektionsmodell für Proportionalsätze.Dreieck mit parallel zur Grundlinie verschiebbarer Schiene und Zahlenteilung zum Einstellen und Vergleichen verschiedener Abschnitte.Modell aus Plexiglas, hochwertiger Kunststoff.

Projektor-Modell eines Drehstromgenerators mit drehbarer Platte.Modell aus Plexiglas, hochwertiger Kunststoff.mit drehbarer Platte

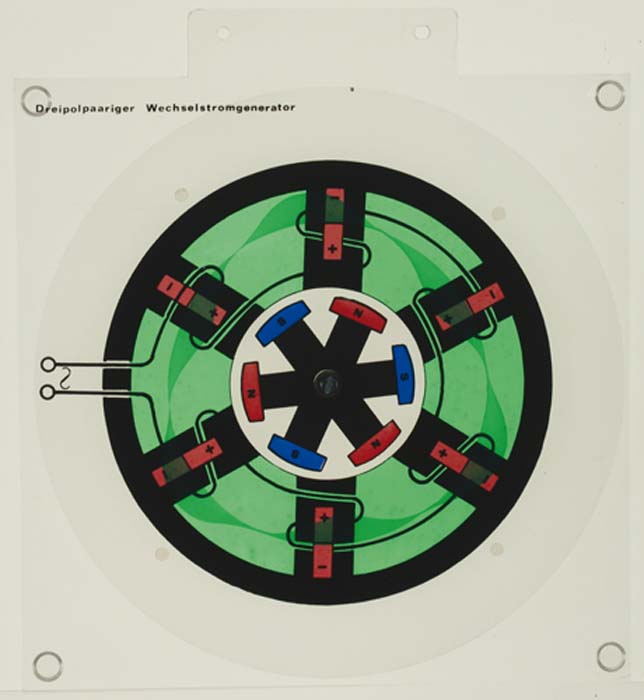
Projektor-Modell eines dreipoligen Wechselstromgenerators mit drehbarer Platte.Modell aus Plexiglas, hochwertiger Kunststoff.mit drehbarer Platte

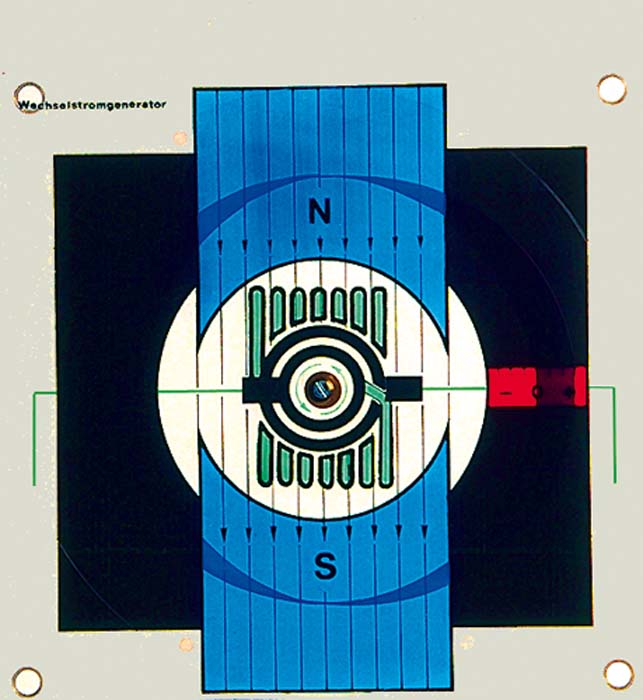
Projektor-Modell eines Wechselstromgeneratorsmit drehbarer Platte.Modell aus Plexiglas, hochwertiger Kunststoff.mit drehbarer Platte

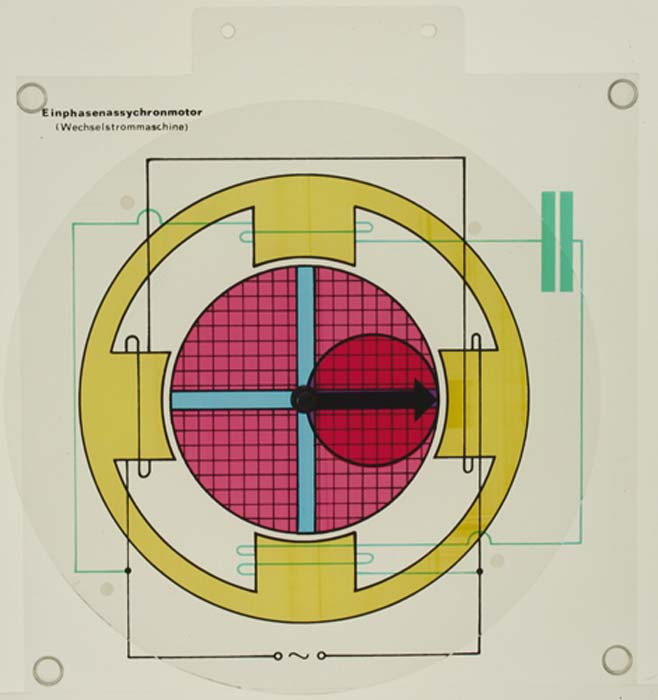
Projektor-Modell eines Einphasenassynchronmotors (Wechselstrommaschine).Modell aus Plexiglas, hochwertiger Kunststoff.(Wechselstrommaschine)

Projektor-Modell Meßschieber, zum Ablesen des Nonius Maßstab 1:2Modell aus Plexiglas, hochwertiger Kunststoff.

Das Domino enthält 8 Einzelspiele mit je 10 Aufgabenstellungen auf der Vorder- und Rückseite der Dominoplättchen mit Übungen zum Kennenlernen und Wiedererkennen der Flächen (allg. Viereck, Quadrat, Rechteck, Raute, Prallelogramm, Drachen, Sechseck, Dreieck, rechtwinkliges Dreieck, Kreis) in unterschiedlichen Größen, räumlichen Lagen bzw. Anordnungen und an vorgegebenen Kriterien. Jedes Dominospiel sollte mit dem Startplättchen begonnen werden. Sind alle 10 Aufgaben richtig gelöst ergeben die Buchstaben auf den Plättchen ein Lösungswort. Die Ordnungssymbole (Kreis, Quadrat, Dreieck und Stern) helfen bei der Unterscheidung der Einzelspiele. Die aus Kunststoff gefertigten Dominoplättchen werden in einer Box geliefert.8 Spiele zum Kennenlernen und Wiedererkennen von Flächenformen

Brüchelabor - Ergänzungsset A Der stapelbare Brüchehalter erlaubt es, durch den transparenten Boden hindurch verschiedene, durch Kreissegmente gebildete Brüche miteinander zu vergleichen. So werden nicht nur Brücheverhältnisse veranschaulicht, sondern auch Addition und Subtraktion von Brüchen aufgezeigt. Schulform: Grundschule, Grundschule 5/6 Schulfach: Mathematik Klassenstufe: 5. Schuljahr bis 6. Schuljahr Abmessung: 27,9 x 19,5 cm Einbandart: Kasten/Kiste2 Brüchehalter

Brüchelabor - Ergänzungsset B Die Arbeit mit dem Brüchelabor unterstützt die Einsicht in den Bereichen Visualisieren und Lesen-Schreiben von echten Brüchen, Gleichwertigkeit von Brüchen, Addition und Subtraktion mit Brüchen. Schulform: Grundschule, Grundschule 5/6 Schulfach: Mathematik Klassenstufe: 5. Schuljahr bis 6. Schuljahr Abmessung: 27,9 x 19,5 cm Einbandart: Kasten/KisteBruch-Teile, gleiche Stückelung wie im Brüchelabor

Brüchelabor - Ergänzungsset C Die Folienscheiben zu verschiedenen Brücheeinheiten dienen der Selbstkontrolle und der Überprüfung von Überlegungen und Berechnungen Schulform: Grundschule, Grundschule 5/6 Schulfach: Mathematik Klassenstufe: 5. Schuljahr bis 6. Schuljahr Abmessung: 27,9 x 19,5 cm Einbandart: Box15 bedruckte Folienscheiben, gleiche Auswahl wie im Brüchelabor

Brüchelabor - Die Welt der Brüche entdecken Die pfiffigen Arbeitsblätter lassen Kinder systematisch die Welt der Brüche entdecken. Auf verständliche Weise wird in die Bedeutung und Benennung von Nenner und Zähler eingeführt. Zahlreiche Beispiele veranschaulichen die Anwendung des Materials aus dem Brüchelabor, vom Kürzen und Erweitern bis hin zum Addieren und Subtrahieren von Brüchen. Mit humorvollen Zeichnungen, Aufgabenstellungen und Spielvorschlägen werden die Kinder altersgemäß motiviert, sich mit dem Thema Brüche auseinanderzusetzen. Zusammen mit dem Brüchelabor bilden die Arbeitsblätter ein ansprechendes Materialpaket, das sowohl im Regelunterricht wie in der Einzelförderung oder Therapie einsetzbar ist. Inhalt: - ca. 44 Schülerarbeitsblätter und 14 Seiten Spielvorlagen als Kopiervorlagen - Reichhaltige Lehrerkommentare und Einsatztipps mit Zusatzhinweisen zum therapeutischen Arbeiten - Lösungen zu den Arbeitsblättern. - Insgesamt ca. 84 Seiten A4. Schulform: Grundschule, Grundschule 5/6 Schulfach: Mathematik Klassenstufe: 5. Schuljahr bis 6. Schuljahr Abmessung: 29,7 x 21,0 cm Einbandart: Broschur Beispielseite-BrüchelaborSchülerarbeitsblätter zum Brüchelabor Bespielseite-5222385.pdf

Messen: Temperaturen, Gewichte, Längen - Experimentierbox Diese Box ist eine leicht transportable Messgeräte-Sammlung, die in der Grundschule überall da eingesetzt werden kann, wo die Größen Temperatur, Gewicht und Länge gemessen werden sollen. Sie bewährt sich im Sachunterricht bei physikalischen und biologischen Untersuchungen, aber auch im Mathematikunterricht. Die Schüler können ein grundschul- und zeitgemäßes Wissen über Maß-Konventionen sowie die Funktionsweise und Benutzung von Messgeräten erwerben. In einem Mess-Triathlon weisen sie nach, dass sie das passende Messgerät auswählen, sachgerecht benutzen und die Ergebnisse notieren können. Dazu dient als Arbeitsvorlage eine Lernstationsreihe, mit der die Kinder den Gebrauch der Messgeräte erlernen und trainieren können. Abmessungen des Koffers: 540 x 450 x 150 mm Die Stationen aus dem Heft Wir üben messen Temperaturen, Gewichte, Längen Temperaturen messen Celsius und Fahrenheit erfinden Thermometerskalen Wir bauen selbst ein Thermometer Ablesetrainer für Thermometerskalen selbst bauen Ableseaufgaben für Thermometer selbst stellen Unser Stationskarton für Temperatur-Mixer Temperaturen zu Hause messen Aufgaben für Mess-Meister Gewichte messen Wiegen mit der Balkenwaage Das Zusammenzählen von Gewichten trainieren Ideen für das Wiegen mit der Balkenwaage Eine Wippenwaage selbst bauen Unser Stationskarton Wiegen mit der Balkenwaage Schnellwaagen durchschauen und richtig benutzen Unser Stationskarton Wiegen mit der Schnellwaage Aufgaben für Mess-Meister Längen messen Woher weiß man, wie lang ein Meter ist? Ein Maßband für die Hosentasche selbst bauen Wir messen uns gegenseitig Messaufgaben mit dem Maßband Unser Stationskarton Messen mit dem Maßband Messen mit dem Mess-Schieber aus der Box Münzen messen mit dem Mess-Schieber Einen Mess-Schieber selbst bauen Unser Stationskasten Messen mit dem Mess-Schieber Eine Aufgabe für Mess-Meister Inhalt: Temperatur messen - Thermometer mit Celsius- und Fahrenheitskala Messbereich 10 bis +50 °C - Thermometer mit Winkelskala Messbereiche 50 und 100 °C - Aufbauthermometer bestehend aus: Erlenmeyerkolben Gummistopfen Kapillare Farbigen Markierungsklammern Trichter zum Befüllen Auffangschalen - Becher für Mischversuche - Gerätebeschreibung - Lernen an Stationen Wir üben messen; Temperaturen, Gewichte, Längen Gewichte messen - Balkenwaage bestehend aus: Waagensäule Waagebalken mit Tarierschieber Bügeln und Waagschalen - Gewichtssatz mit 0,1 g, 1g und 10 g Gewichtsstücken - Schnellwaagen, Messbereich 100 g und 500 g - Federwaage, Messbereich 5 kg - Luftballons mit Schnur Längen messen - Maßband in Kapsel, 1,5 m lang - Lineal mit cm- und inch-Teilung, 30 cm lang - Messschieber ohne Noniusskala, - Messbereich 15 cm mit Innen-, Außen- und Tiefenmaß - Metrilog zum Abrollen von StreckenMaterial für 3 x 6 Gruppen

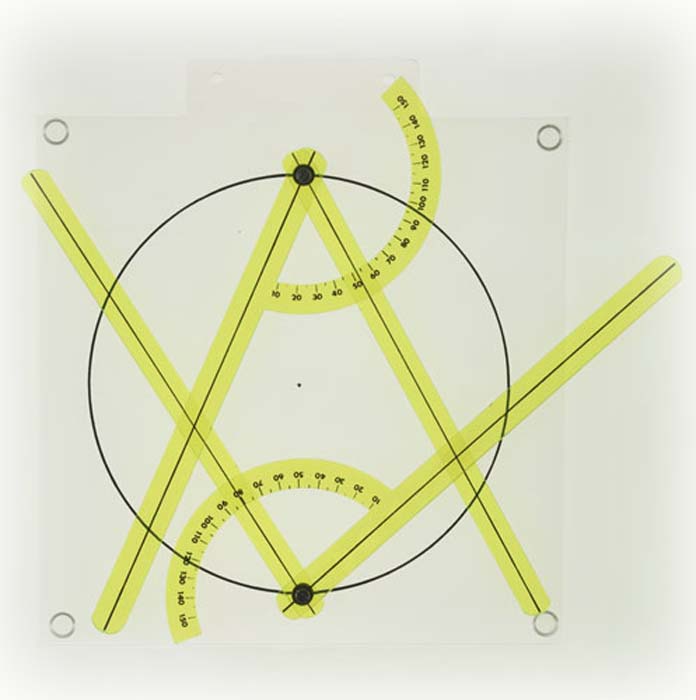
Durch eine manuell eingeleitete positive oder negative Drehrichtung eines Zahnrades wird ein Zeigersystem in Bewegung gesetzt. Mit einem Lineal, dessen Maßstab auf den Einheits-Radius R = 1 abgestimmt ist, können, entsprechend der mathematischen Definitionen für jeden beliebigen Zentrumswinkel, die Strecken für die dazugehörigen Winkelfunktions-Werte abgemessen werden. Durch ein Zahnradgetriebe ist eine Feineinstellung des Zentrumwinkels gewährleistet. zur optisch-dynamischen Darstellung der im Zusammenhang stehenden Winkelfunktionen sin, cos, tan, cot am Einheitskreis (R = 1).